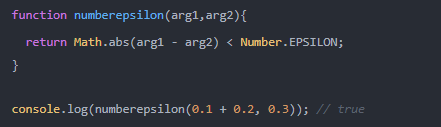
为什么0.1+0.2 ! == 0.3,如何让其相等

在开发过程中遇到类似这样的问题:

这里得到的不是想要的结果,要想等于0.3,就要把它进行转化:

toFixed(num) 方法可把 Number 四舍五入为指定小数位数的数字。那为什么会出现这样的结果呢?
计算机是通过二进制的方式存储数据的,所以计算机计算0.1+0.2的时候,实际上是计算的两个数的二进制的和。0.1的二进制是0.0001100110011001100...(1100循环),0.2的二进制是:0.00110011001100...(1100循环),这两个数的二进制都是无限循环的数。那JavaScript是如何处理无限循环的二进制小数呢?
一般我们认为数字包括整数和小数,但是在 JavaScript 中只有一种数字类型:Number,它的实现遵循IEEE 754标准,使用64位固定长度来表示,也就是标准的double双精度浮点数。在二进制科学表示法中,双精度浮点数的小数部分最多只能保留52位,再加上前面的1,其实就是保留53位有效数字,剩余的需要舍去,遵从“0舍1入”的原则。
根据这个原则,0.1和0.2的二进制数相加,再转化为十进制数就是:0.30000000000000004。
下面看一下双精度数是如何保存的:
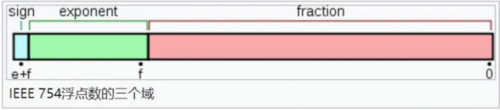
第一部分(蓝色):用来存储符号位(sign),用来区分正负数,0表示正数,占用1位第二部分(绿色):用来存储指数(exponent),占用11位第三部分(红色):用来存储小数(fraction),占用52位
对于0.1,它的二进制为:

转为科学计数法(科学计数法的结果就是浮点数):

可以看出0.1的符号位为0,指数位为-4,小数位为:

那么问题又来了,指数位是负数,该如何保存呢?
IEEE标准规定了一个偏移量,对于指数部分,每次都加这个偏移量进行保存,这样即使指数是负数,那么加上这个偏移量也就是正数了。由于JavaScript的数字是双精度数,这里就以双精度数为例,它的指数部分为11位,能表示的范围就是0~2047,IEEE固定双精度数的偏移量为1023。
当指数位不全是0也不全是1时(规格化的数值),IEEE规定,阶码计算公式为 e-Bias。 此时e最小值是1,则1-1023= -1022,e最大值是2046,则2046-1023=1023,可以看到,这种情况下取值范围是-1022~1013。当指数位全部是0的时候(非规格化的数值),IEEE规定,阶码的计算公式为1-Bias,即1-1023= -1022。当指数位全部是1的时候(特殊值),IEEE规定这个浮点数可用来表示3个特殊值,分别是正无穷,负无穷,NaN。 具体的,小数位不为0的时候表示NaN;小数位为0时,当符号位s=0时表示正无穷,s=1时候表示负无穷。
对于上面的0.1的指数位为-4,-4+1023 = 1019 转化为二进制就是:1111111011.
所以,0.1表示为:

说了这么多,是时候该最开始的问题了,如何实现0.1+0.2=0.3呢?
对于这个问题,一个直接的解决方法就是设置一个误差范围,通常称为“机器精度”。对JavaScript来说,这个值通常为2-52,在ES6中,提供了Number.EPSILON属性,而它的值就是2-52,只要判断0.1+0.2-0.3是否小于Number.EPSILON,如果小于,就可以判断为0.1+0.2 ===0.3